LLM Model Parameter & Memory Required for Training and Inference
Machines only understand numbers, data such as text and images is converted into vectors. The vector is the only format that is understood by neural networks and transformer architectures.
Token
Tokens serve as the basic data units. In the context of text, a token can be a word, part of a word (subword), or even a character — depending on the tokenization process.
Ex “The evil that men do lives after them” would become: | 791 | 14289 | 430 | 3026 | 656 | 6439 | 1306 | 1124 |.
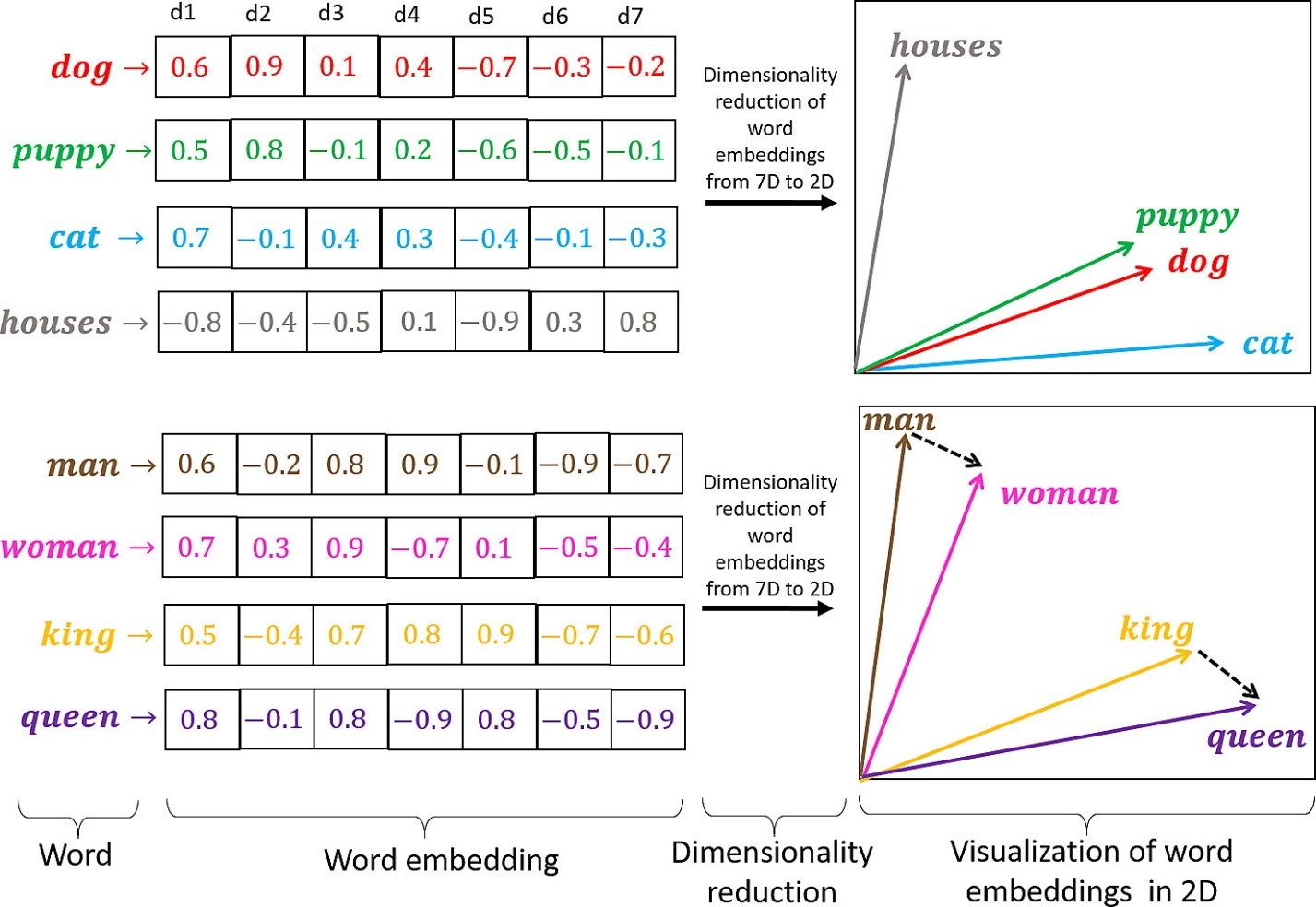
Vectors
Vectors provide a mathematical framework for machine processing. Vectors are used to represent text or data in a numerical form that the model can understand and process.
Embeddings
To capture the meaning and semantic relationships between tokens, LLMs employ token encoding techniques. These techniques transform tokens into dense numerical representations called embeddings. Embeddings encode semantic and contextual information, enabling LLMs to understand and generate coherent and contextually relevant text. Advanced architectures like transformers use self-attention mechanisms to learn dependencies between tokens and generate high-quality embeddings.
Tokens are encoded or decoded by a tokenizer; an embeddings model is responsible for generating text embeddings in the form of a vector. Embeddings are what allow LLMs to understand the context, nuance and subtle meanings of words and phrases. They are the result of the model learning from vast amounts of text data, and encode not just the identity of a token but its relationships with other tokens.
Token Limit
The token limit is the maximum number of tokens that can be used in the prompt and the completion of the model. Most LLMs have token limits, which refer to the maximum number of tokens that the model can process at once. The token limit is determined by the architecture of the model
Token processing cost
Each token that the model processes requires computational resources – memory, processing power, and time. Thus, the more tokens a model has to process, the greater the computational cost
Parameters
We can think of parameters as internal settings or dials within a large language model that can be adjusted to optimize the process of taking tokens and generating new ones
When training a large language model, parameters are features of the LLM that are adjusted in order to optimize the model’s ability to predict the next token in a sequence
simplified explanation of how parameters are trained and function:
A model’s parameters are set to an initial value, either randomly or based on previous training.
The large language model being trained is fed vast amounts of textual data.
As the model is trained, it takes the input and makes a prediction about what the correct output must be.
In training, the LLM compares its prediction to the actual text to see if it predicted correctly or not. The model “learns” from its mistakes and adjusts its parameters if its prediction was incorrect.
This process continues for millions or billions of examples, with the model adjusting its parameters each time and increasing its accuracy in prediction.
Through this iterative process of prediction, error checking, and parameter adjustment, the LLM becomes more accurate and sophisticated in its language abilities.
LMs are complex systems with many different parameters. These parameters govern how the model learns and generates text. Some of the most important parameters for LLMs include:
Model size
The model size is the number of parameters in the LLM. The more parameters a model has, the more complex it is and the more data it can process. However, larger models are also more computationally expensive to train and deploy.
Training data
The training data is the dataset that the LLM is trained on. The quality and quantity of the training data has a significant impact on the performance of the model.
Hyperparameters
Hyperparameters are settings that control how the LLM is trained. These settings can be fine-tuned to improve the performance of the model on specific tasks.
Parameter types
1. float: 32-bit floating point, 4 bytes
2. half/BF16: 16-bit floating point, 2 bytes
3. int8: 8-bit integer, 1 byte
4. int4: 4-bit integer, 0.5 bytes
1 Billion Parameters = 4 x 10E9 bytes = 4GB
LLM has 70B parameters, it means that the model has 70 billion adjustable parameters. These parameters are used to learn the relationship between words and phrases in the training data. The more parameters a model has, the more complex it can be and the more data it can process. However, larger models are also more computationally expensive to train and deploy
Is more parameters always better?
The short answer is no.
A model with fewer parameters that is trained on high quality data will outperform a larger model trained on low quality data. In other words, the quality of the data used to train a model is just as important as the size of the model itself.
Inference Memory Estimation
For a 1 billion parameter model (1B), the estimated memory requirements are as follows:
— 4 GB for float precision, 2 GB for BF16 precision, and 1 GB for int8 precision. This estimation can be applied to other versions accordingly.
Memory Required for Training
A conservative estimate is about four times the memory needed for inference with the same parameter count and type. For example, training a 1B model with float precision would require approximately 16 GB (4 GB * 4).
· Gradients
Memory required for gradients is equal to the number of parameters.
· Optimizer States
The memory needed for the optimizer states depends on the type of optimizer used.
AdamW optimizer -twice the number of parameters, SGD optimizer -memory equivalent to the number of parameters is needed.
Memory Usage with LoRA/QloRA Techniques
LoRA involves running inference on the original model and training a smaller model to achieve nearly the same effect as training the original parameters.
For instance, if you need to fine-tune parameters of size 1024×512, using LoRA with a chosen Rank of 8, you only need to fine-tune the following number of parameters: 1024×8 + 512×8.
This process requires running inference on the original parameter volume once (without needing gradients and optimizer states), but it still requires some memory to store data during the computation. The total memory used is the sum of these requirements.
Estimate Memory Usage for Inference
1B-BF16 model would need memory equal to the number of parameters multiplied by the size of the type: 1 billion parameters * 2 bytes = 2 billion bytes.
2 billion bytes = 2 * 1,000 * 1,000 * 1,000 / 1024 / 1024 / 1024 ≈ 2 GB (considering 1000/1024)³ ≈ 0.93.
Estimate Memory Usage for Training
Back-propagation, Adam optimization, and Transformer architecture, the memory required for training is typically 3 to 4 times that needed for inference of an LLM of the same size. A conservative estimate is to calculate using a factor of 4
float type parameters: 1(billion parameters) * 4 (bytes per float parameter) * 4 = 16 GB